Retrospective analysis and forecasting of the spread of viruses in real time: the case of COVID-19 in St. Petersburg and Moscow in 2020–2021
- Authors: Zakharov V.V.1, Balykina Y.E.1
-
Affiliations:
- St. Petersburg State University
- Issue: Vol 69, No 6 (2024)
- Pages: 500-508
- Section: ORIGINAL RESEARCHES
- URL: https://virusjour.crie.ru/jour/article/view/16682
- DOI: https://doi.org/10.36233/0507-4088-265
- EDN: https://elibrary.ru/faiopq
- ID: 16682
Cite item
Abstract
The aim of the study is to apply mathematical methods to generate forecasts of the dynamics of random values of the percentage increase in the total number of infected people and the percentage increase in the total number of recovered and deceased patients. The obtained forecasts are used for retrospective forecasting of COVID-19 epidemic process dynamics in St. Petersburg and in Moscow.
Materials and methods. When conducting a retrospective analysis and forecasting the dynamics of the total number of cases and the dynamics of the total number of patients who have either died or recovered, the values of percentage increases in these indicators were used. Retrospective analysis and forecasting of the dynamics of the COVID-19 epidemic process were carried out over 14-day time intervals, starting from March 25, 2020 to January 20, 2021, using the time series forecasting method proposed by the authors.
Results and discussion. The retrospective two-week forecasts of the total number of cases and the number of active cases presented in the paper demonstrated a high accuracy performance, both in Moscow and St. Petersburg. The MAPE (mean absolute percentage error) for the total number of cases at the peaks of incidence, generally, did not exceed 1%. It is shown that the accuracy of the obtained retrospective forecasts of the total number of cases in St. Petersburg, built starting from May 2020, has increased significantly compared to the April forecasts. A similar conclusion can be made regarding the forecasts of the total number of cases in Moscow in April and May 2020.
Full Text
Introduction
The epidemic of a new coronavirus infection (COVID-19) in the Russian Federation, which started in March 2020, involved the population of all regions of the country in the epidemic process. By the end of December 2020, more than 3 million COVID-19 cases had been registered in the country. This pace of the epidemic has resulted in a significant increase in the burden on the health care system. At the same time, the problem of the lack of effective methods for predicting the dynamics of the spread of the new virus, a parameter that had not yet been studied, also became an issue. The World Health Organization (WHO) recognizes that the availability of adequate mathematical models of virus spread and the development of methods for predicting epidemic dynamics can play a key role in informing decision-making by health resource and policy makers. Such models help to provide insights into the future dynamics of infectious disease spread and the potential role of different types of public health intervention strategies [1, 2]. Many researchers use a three-compartment SIR model to describe the processes of infectious disease spread. The population of a country where an infection is spreading is divided into 3 groups (compartments): Susceptible, Infected and Removed (recovered or deceased). It is assumed that the population of the country is equal to the sum of the numbers of these 3 groups. The model was first described in a general form in the study by W. Kermack and A. McKendrick in 1927 [3], but the greatest interest of researchers was further focused on the special case of this model in the form of a system of 3 differential equations with constant coefficients [4]. Some specialists prefer the SIR model because of the small number of parameters required as inputs and the wide possibilities for applying traditional classical approaches to modeling and using computational algorithms. However, this advantage simultaneously becomes a disadvantage, since the simplification of the model generates inaccuracy of the forecasts obtained on their basis compared to the actual values of the main variables of the epidemic process [5–7]. A number of articles [8–11] provide examples of the application of the ARIMA autoregressive model in the generation of forecasts of pandemic spread in a number of countries of the world. It is noted that this model, compared to other tools, provides more accurate forecasts; however, although time series models are a popular forecasting tool, their application to assess the spread of new infections does not always make it possible to build forecasts with a high degree of accuracy.
In addition to different varieties of ARIMA family models, various machine learning techniques, including decision trees and ensemble models such as random forest and gradient boosting, can also be used to predict COVID-19 dynamics [12, 13]. These techniques can take into account many factors, including infection rates, population mobility, and social distance measures applied. Artificial neural networks are also widely used due to their ability to process time series and make predictions from sequential data [14–16].
Several articles [17–20] have been devoted to the study of the regularities of epidemic spread of SARS-CoV-2 at the initial stage of the COVID-19 pandemic in the Russian Federation, Moscow and St. Petersburg in 2020, in which a number of important periods in the dynamics of detecting new cases of COVID-19 have been identified: an increase in incidence, a period of epidemic quiescence, a period of epidemic rise, and a period of persistently high incidence of COVID-19. It should be noted that an important motivation for the present study was, among other things, publications on the contribution of Academician V.D. Belyakov [21, 22] to the development of ideas about a unified (“general medical” in his definition) epidemiology including non-communicable diseases. In earlier articles [23–25], the authors of this article proposed an approach, the main idea of which is to first forecast future predictive trends of stochastic parameters of the epidemic process, and then to calculate future trajectories of the main variables of this process.
The aim of this study is to generate forecasts of the dynamics of time series of random values of the percentage increase in the total number of infected people and the percentage increase in the total number of patients who recovered and died, and to describe the results of using the methods developed by the authors for retrospective forecasting of the dynamics of epidemic processes in St. Petersburg and Moscow.
Materials and methods
The study was carried out by the scientific team of the Center for Analysis of Dynamic Processes and Systems at St. Petersburg State University. When conducting computational experiments to predict the dynamics of the COVID-19 epidemic process in St. Petersburg in the period from March 2020 to June 2020 and in Moscow from September 2020 to January 2021, we used time series data of the official registration of the daily number of new cases of the disease and the number of cases of completion of the disease (recovery or death of patients), presented on the website стопкоронавирус.рф and statistical data from the CSSE Center of Johns Hopkins University 1.
In terms of mathematical statistics, data on new cases of disease form a time series of xinf(t) (the number of new cases on day t, and data on the number of cases of disease outcomes (patients recovered or deceased) form a time series of xof(t), where t – is a particular day of the epidemic. Let us denote by Xinf(t) the total number of confirmed cases from the beginning of the epidemic up to and including day t, and by Xof(t) – the total number of patients who underwent the disease by that day. The resulting time series Xinf(t) and Xof(t) are called the integral form of the time series xinf(t) and xof(t) respectively. The expression of the trend in the dynamics of new cases of the disease (growth/decline) is usually described by the method proposed by V.D. Belyakov [26]. It should be noted that since the members of the time series xinf(t) take random values, which can increase or decrease, the percentage increase in the number of new cases, as well as the growth/decrease trend, can take both negative values and positive values (or equal to 0). We denote the percentage increase in the number of new cases on day t relative to the number of new cases on day t – 1 by r(t) and calculate it according to the following formula:
The upward/downward trend in the number of new cases is described as the average percentage increase over specified time intervals and is used as an important characteristic in monitoring the epidemic process [17]. However, its use in predicting the future dynamics of the epidemic process in real time is problematic, mainly because its values randomly change sign from plus to minus. It can be observed that the time series Xinf(t) and Xof(t), unlike the time series xinf(t) and xof(t), are non-negative and increase with time. In the present study, we considered the percentage increase in the total number of patients rinf(t) and the percentage increase rof(t) in the total number of patients for whom the disease has ended as the main parameters of the epidemic process dynamics [23–25]. The values of these parameters for any day t of the epidemic can be calculated using the following formulas:
Given that the numerator and denominator of the presented formulas are terms of time series; the indicated percentage increases also form a time series of random variables. During an epidemic, the total number of cases and the total number of patients who have underwent the disease tend to increase strictly, so the values of these parameters can be considered positive for any day except for the day on which the number of new cases is 0. Furthermore, if the percentage increase rinf(t) is greater than the percentage increase rinf(t – 1), then it is expressed with the following inequality
or similarly:
From the last inequality we can conclude that as the percentage increase in the total number of cases increases, the number of new cases also increases. However, the statement that the number of new cases decreases as the percentage increase in the total number of cases decreases is not always true.
The same is true for the percentage increase in the total number of patients who recovered and those who died. Another trend that can be found when analyzing incidence statistics in St. Petersburg and Moscow in May 2020 is that the decline in the percentage increase in the total number of cases began about a week before the peak in the number of new cases. The same situation was repeated in December 2020. Therefore, we believe that monitoring the dynamics of changes in the percentage increase in the total number of cases is essential in forecasting the dynamics of both the total number of cases and new cases of the disease.
For the purposes of this study, 20 consecutive 2-week retrospective projections of the percentage increase in the total number of infected people and the percentage increase in the total number of completed cases were generated for the 2020 year statistics in St. Petersburg and Moscow.
Referring to Table, it can be observed that the percentage increase in the total number of infected people in St. Petersburg after April 22, 2020 has a clear downward trend. The same situation was observed in Moscow. A similar trend, although of a less pronounced nature and with a lag of 2–3 weeks, has a percentage increase in the total number of patients for whom the disease has ended.
Table. Total number of registered COVID-19 cases in St. Petersburg in April–June 2020
Таблица. Общее количество заболевших COVID-19 в Санкт-Петербурге в апреле–июне 2020 г.
Date Дата | Total number of cases, abs. Общее число заболевших, абс. | rinf(t), % | Date Дата | Total number of cases, abs. Общее число заболевших, абс. | rinf(t), % |
12.04.2020 | 557 | 14.14 | 21.05.2020 | 12 203 | 3.46 |
13.04.2020 | 678 | 21.72 | 22.05.2020 | 12 592 | 3.19 |
14.04.2020 | 799 | 17.85 | 23.05.2020 | 12 955 | 2.88 |
15.04.2020 | 929 | 16.27 | 24.05.2020 | 13 339 | 2.96 |
16.04.2020 | 1083 | 16.58 | 25.05.2020 | 13 713 | 2.80 |
17.04.2020 | 1507 | 39.15 | 26.05.2020 | 14 076 | 2.65 |
18.04.2020 | 1646 | 9.22 | 27.05.2020 | 14 463 | 2.75 |
19.04.2020 | 1760 | 6.93 | 28.05.2020 | 14 846 | 2.65 |
20.04.2020 | 1846 | 4.89 | 29.05.2020 | 15 215 | 2.49 |
21.04.2020 | 1973 | 6.88 | 30.05.2020 | 15 580 | 2.40 |
22.04.2020 | 2267 | 14.90 | 31.05.2020 | 15 949 | 2.37 |
23.04.2020 | 2458 | 8.43 | 01.06.2020 | 16 313 | 2.28 |
24.04.2020 | 2711 | 10.29 | 02.06.2020 | 16 689 | 2.30 |
25.04.2020 | 2926 | 7.93 | 03.06.2020 | 17 069 | 2.28 |
26.04.2020 | 3077 | 5.16 | 04.06.2020 | 17 444 | 2.20 |
27.04.2020 | 3238 | 5.23 | 05.06.2020 | 17 822 | 2.17 |
28.04.2020 | 3436 | 6.11 | 06.06.2020 | 18 169 | 1.95 |
29.04.2020 | 3726 | 8.44 | 07.06.2020 | 18 509 | 1.87 |
30.04.2020 | 4062 | 9.02 | 08.06.2020 | 18 835 | 1.76 |
01.05.2020 | 4411 | 8.59 | 09.06.2020 | 19 153 | 1.69 |
02.05.2020 | 4734 | 7.32 | 10.06.2020 | 19 466 | 1.63 |
03.05.2020 | 5029 | 6.23 | 11.06.2020 | 19 769 | 1.56 |
04.05.2020 | 5346 | 6.30 | 12.06.2020 | 20 043 | 1.39 |
05.05.2020 | 5572 | 4.23 | 13.06.2020 | 20 305 | 1.31 |
06.05.2020 | 5884 | 5.60 | 14.06.2020 | 20 561 | 1.26 |
07.05.2020 | 6190 | 5.20 | 15.06.2020 | 20 813 | 1.23 |
08.05.2020 | 6565 | 6.06 | 16.06.2020 | 21 047 | 1.12 |
09.05.2020 | 6990 | 6.47 | 17.06.2020 | 21 275 | 1.08 |
10.05.2020 | 7404 | 5.92 | 18.06.2020 | 21 506 | 1.09 |
11.05.2020 | 7711 | 4.15 | 19.06.2020 | 21 734 | 1.06 |
12.05.2020 | 8050 | 4.40 | 20.06.2020 | 21 966 | 1.07 |
13.05.2020 | 8485 | 5.40 | 21.06.2020 | 22 195 | 1.04 |
14.05.2020 | 8945 | 5.42 | 22.06.2020 | 22 412 | 0.98 |
15.05.2020 | 9486 | 6,05 | 23.06.2020 | 22 632 | 0.98 |
16.05.2020 | 10 011 | 5.53 | 24.06.2020 | 22 850 | 0.96 |
17.05.2020 | 10 462 | 4.51 | 25.06.2020 | 23 071 | 0.97 |
18.05.2020 | 10 887 | 4.06 | 26.06.2020 | 23 294 | 0.97 |
19.05.2020 | 11 340 | 4.16 | 27.06.2020 | 23 518 | 0.96 |
20.05.2020 | 11 795 | 4.01 | 28.06.2020 | 23 735 | 0.92 |
Our method of making a forecast on a specific given day involves, at the 1st stage, the selection of a suitable function (linear, power or exponential) to approximate the values of the percentage increases rinf(t) and rof(t) for the preceding 14 days before the day of making the forecast. After completion of step 1, the selected approximating function was used to calculate the forecast values of percentage increases inf(t) and of(t) for the next 14 days following the day of forecast generation. The obtained values of percentage increases were used to calculate, within the forecasting horizon, the forecast values of inf(t) and of(t) with the following formulas:
For each day t of the forecasting interval, we can calculate the deviation e(t) of the forecast value from the actual value, e.g:
and the absolute forecast error:
The MAPE (mean absolute percentage error), which is often used in statistics, was chosen as the average forecast error for each forecast interval. MAPE values were calculated for a forecasting interval of 14 days by the formula:
Results
The results of the computational experiments are presented in Tables 1–8S in the Appendix. Tables 1–3S show the forecasts of the dynamics of percentage increases in the total number of patients in St. Petersburg since the beginning of the epidemic, generated on April 8 and 22, May 6 and 20, June 3 and 17, 2020.
The average MAPE error for the forecast of the total number of infected people, generated on April 8, 2020, is 5.15%, while the error for the forecast on April 22 is equal to 19.66%. Thus, the accuracy of the forecasts of the total number of infected people in April was not very high. The average MAPE error for the forecast generated on May 6, 2020 is 4.52% (Fig. 1). It should be noted that the June forecasts presented in Table 3S already have higher accuracy than the May forecasts.
Fig. 1. Two-week forecasts of the total number of cases in St. Petersburg in May 2020.
Рис. 1. Двухнедельные прогнозы общего количества заболевших в Санкт-Петербурге в мае 2020 г.
The MAPE error for the June 3, 2020 forecast is equal to 3.17%, while the error for the June 17 forecast is 0.77%.
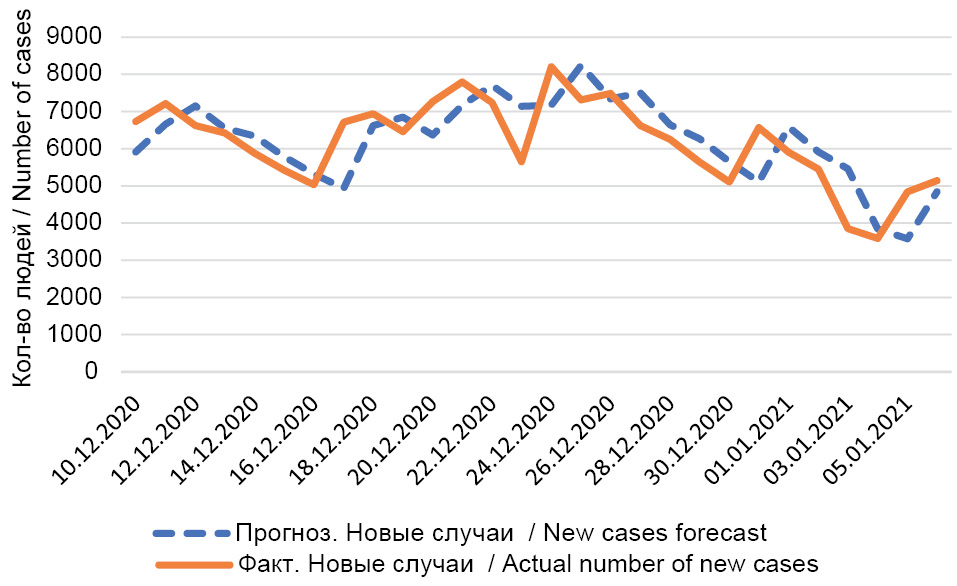
Data on certain forecasts during the fall and winter period in Moscow are shown in Tables 3S and 6S. The MAPE error for the forecast in Moscow made on November 25, 2020 is equal to 0.13%, while the error for the forecast made on December 9 is equal to 0.13%. The MAPE error for the forecast made on December 23, 2020 is equal to 0.17%, while the error for the forecast made on January 6, 2021 is equal to 0.30% (Fig. 2).
Fig. 2. Two-week forecasts of the total number of cases in Moscow in December 2020.
Рис. 2. Двухнедельные прогнозы общего количества заболевших в Москве в декабре 2020 г.
It is well known that the number of active cases on any given day can be calculated by subtracting the total number of patients who recovered and the total number of patients who died from the total number of cases. The predicted number of active cases was calculated as the difference between the predicted total number of cases and the predicted total number of patients who underwent the disease. Fig. 3 and Table 6S show the predicted and actual values of the number of active cases in St. Petersburg during the epidemic peak in May 2020. Table 7S contains data on forecasts of the number of new cases and the number of active cases in Moscow from December 24, 2020 to January 6, 2021 during the epidemic peak period (Figs. 4, 5). The maximum values of actual and forecasted values of active cases in the vicinity of the epidemic peaks of the first and second wave are highlighted in bold in the tables.
Fig. 3. Forecast of the number of active cases in St. Petersburg in May–June 2020.
Рис. 3. Прогноз количества активных случаев болезни в Санкт-Петербурге в мае–июне 2020 г.
Fig. 4. Forecast of the number of active cases in Moscow in December 2020.
Рис. 4. Прогноз количества активных случаев болезни в Москве в декабре 2020 г.
Fig. 5. Forecast of new cases in Moscow in December 2020.
Рис. 5. Прогноз новых случаев болезни в Москве в декабре 2020 г.
In order to assess the possibility of predicting a sharp increase in incidence when the Delta strain spreads in Moscow in June 2021, we turned to statistical data on the dynamics of COVID-19 for this period. A sharp increase in incidence was observed from June 8 to June 15, 2021. Monitoring of the dynamics of the percentage increase in the total number of confirmed cases showed that the change in the trend of steady decrease in the percentage increase was observed until June 2, then its value stopped for 3 days at 0.24%, after which the percentage increase began to increase. By June 8 the value of the percentage increase has already reached the level of 0.32%. Such a rapid rise in the percentage increase within 4 days, in our opinion, may indicate a possible further exponential growth of the percentage increase and the number of new cases. The retrospective forecast biult on June 8 for 6 days using our proposed methods is shown in Table 8S and Fig. 6. It has a MAPE error of 0.06% for total cases and 10.41% for new cases.
Fig. 6. Forecast of new cases in during the spread of delta strain in Moscow in June 2021.
Рис. 6. Прогноз новых случаев при распространении штамма дельта в Москве в июне 2021 г.
Discussion
Computational experiments showed that in April 2020, the dynamics of the percentage increase in the total number of cases in St. Petersburg was difficult to predict, but the forecasts made in May-June were already quite accurate. The accuracy of the obtained retrospective forecasts of the total number of the infected people, generated in May 2020, has significantly increased in comparison with April (Table 2S and Fig. 1). In our opinion, this can be explained by the fact that the selected forecasting method passed the stage of training on current data in April and then was adapted to use for the new data obtained in May. It can be concluded that the uncertainty in estimating the future dynamics of the epidemic process by the beginning of May was significantly reduced. The effectiveness of the proposed forecasting method was also confirmed when generating retrospective 2-week forecasts in Moscow (Tables 4S and 4S, Fig. 2). It should be noted that during the periods of the beginning of the spread of more virulent strains of COVID-19 and during the introduction of strict measures to counteract the spread of the epidemic, the accuracy of the method proposed in this article may be limited. Such situations require additional study. In the framework of the present study, computational experiments were conducted to generate 2-week retrospective forecasts not only of the dynamics of the total number of infected people, but also forecasts of the dynamics of the number of daily new cases, the total number of patients who underwent the disease, and the number of active cases (the current number of infected people). The forecasting results demonstrated quite high accuracy of the obtained forecasts. As examples, Tables 6S and 7S also show data on forecasts and actual values of the number of active cases during the epidemic peaks in May 2020 in St. Petersburg (Fig. 3) and in December 2020 in Moscow (Fig. 4). These figures show that the predicted values of the number of active cases when approaching the peak of the epidemic differ insignificantly from the actual values. The MAPE error of forecasting active cases in Moscow at the forecast horizon from December 25, 2020 to January 6, 2021 is equal to 6.16%. In the initial period of the rise in incidence, the actual maximum level (10,619) of infected people in St. Petersburg was recorded on June 6, and it was forecasted to be 12,210 active cases and was projected for June 2. The maximum number of new cases during the second incidence upswing in Moscow was predicted to be 8,237 on December 25, 2020, and the actual value (8,203) was recorded on December 24 (Fig. 5). The MAPE error of forecasting new cases in Moscow at the forecast horizon from December 25, 2020 to January 6, 2021 is equal to 15.12%.
Conclusion
The analysis of the dynamics of the daily number of new COVID-19 cases shows that this change in the course of the entire epidemic has a stochastic character, is difficult to predict and, as a consequence, creates significant uncertainty in the assessment of future values of this indicator and the evolution of the epidemic process. The method considered in this paper for predicting future values of percentage increases in the total number of infected people and the total number of patients who have undergone the disease, was tested on statistical data from the portal стопкоронавирус.рф in the period from March 2020 to June 2021. The retrospective 2-week forecasts of the total number of confirmed cases during the two peak periods of the epidemic, when the burden on the health care system was at its highest, made during the computational experiments and described in the paper, demonstrated sufficiently high accuracy. The accuracy of the resulting retrospective forecasts of the total number of cases made in May was significantly improved compared to the accuracy of the April forecasts. In our opinion, this indicates that the selected method for forecasting the dynamics of the percentage increase in the total number of cases was focused on current data in April and then adapted to be used for new data from May 2020. The application of the forecasting method proposed in this study was also quite effective in predicting the dynamics of active cases and new cases in the vicinity of the peaks of the first and second wave epidemics.
1 COVID-19 Data Visualization Center [Internet]. Johns Hopkins Coronavirus Resource Center. Доступно по: https://coronavirus.jhu.edu/data
About the authors
Victor V. Zakharov
St. Petersburg State University
Email: v.zaharov@spbu.ru
ORCID iD: 0000-0002-2743-3880
PhD, Professor, Department of Mathematical Modeling of Energy Systems
Russian Federation, 99034, St. PetersburgYulia E. Balykina
St. Petersburg State University
Author for correspondence.
Email: j.balykina@spbu.ru
ORCID iD: 0000-0003-2143-0440
PhD, Associate Professor, Department of Mathematical Modeling of Energy Systems
Russian Federation, 99034, St. PetersburgReferences
- Foppa I.M. A Historical Introduction to Mathematical Modeling of Infectious Diseases: Seminal Papers in Epidemiology. London: Academic Press; 2016.
- Shinde G.R., Kalamkar A.B., Mahalle P.N., Dey N., Chaki J., Hassanien A.E. Forecasting models for coronavirus disease (COVID-19): A survey of the state-of-the-art. SN Comput. Sci. 2020; 1(4): 197. https://doi.org/10.1007/s42979-020-00209-9
- Kermack W.O., McKendrick A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. (London) A. 1927; 115(772): 700–21. https://doi.org/10.1098/rspa.1927.0118
- Anderson R.M., May R.M. Infectious Diseases of Humans. Dynamics and Control. Oxford: Oxford University Press; 1991.
- Moein S., Nickaeen N., Roointan A., Borhani N., Heidary Z., Javanmard S.H., et al. Inefficiency of SIR models in forecasting COVID-19 epidemic: a case study of Isfahan. Sci. Rep. 2021; 11(1): 4725. https://doi.org/10.1038/s41598-021-84055-6
- Melikechi O., Young A.L., Tang T., Bowman T., Dunson D., Johndrow J. Limits of epidemic prediction using SIR models. J. Math Biol. 2022; 85(4): 36. https://doi.org/10.1007/s00285-022-01804-5
- Dil S., Dil N., Maken Z.H. COVID-19 trends and forecast in the Eastern Mediterranean region with a particular focus on Pakistan. Cureus. 2020; 12(6): e8582. https://doi.org/10.7759/cureus.8582
- Moftakhar L., Seif M., Safe M.S. Exponentially increasing trend of infected patients with COVID-19 in Iran: A comparison of neural network and ARIMA forecasting models. Iran J. Public Health. 2020; 49(Suppl. 1): 92–100. https://doi.org/10.18502/ijph.v49iS1.3675
- Ahmar A.S., Del Val E.B. SutteARIMA: Short-term forecasting method, a case: Covid-19 and stock market in Spain. Sci. Total. Environ. 2020; 729: 138883. https://doi.org/10.1016/j.scitotenv.2020.138883
- Chaudhry R.M., Hanif A., Chaudhary M., Minhas S. 2nd., Mirza K., Ashraf T., et al. Coronavirus disease 2019 (COVID-19): Forecast of an emerging urgency in Pakistan. Cureus. 2020; 12(5): e8346. https://doi.org/10.7759/cureus.8346
- Tandon H., Ranjan P., Chakraborty T., Suhag V. Coronavirus (COVID-19): ARIMA-based time-series analysis to forecast near future and the effect of school reopening in India. J. Health Manag. 2022; 24(3): 373–88. https://doi.org/10.1177/09720634221109087
- Özen F. Random forest regression for prediction of COVID-19 daily cases and deaths in Turkey. Heliyon. 2024; 10(4): e25746. https://doi.org/10.1016/j.heliyon.2024.e25746
- Galasso J., Cao D.M., Hochberg R. A random forest model for forecasting regional COVID-19 cases utilizing reproduction number estimates and demographic data. Chaos Solitons Fractals. 2022; 156: 111779. https://doi.org/10.1016/j.chaos.2021.111779
- Wieczorek M., Siłka J., Woźniak M. Neural network powered COVID-19 spread forecasting model. Chaos Solitons Fractals. 2020; 140: 110203. https://doi.org/10.1016/j.chaos.2020.110203
- Dadyan E., Avetisyan P. Neural networks and forecasting COVID-19. Opt. Mem. Neural Networks. 2021; 30: 225–35. https://doi.org/10.3103/S1060992X21030085
- Tamang S., Singh P., Datta B. Forecasting of COVID-19 cases based on prediction using artificial neural network curve fitting technique. Glob. J. Environ. Sci. Manag. 2020; 6(S): 53–64. https://doi.org/10.22034/GJESM.2019.06.SI.06
- Akimkin V.G., Kuzin S.N., Semenenko T.A., Shipulina O.Yu., Yatsyshina S.B., Tivanova E.V., et al. Patterns of the SARS-CoV-2 epidemic spread in a megacity. Voprosy virusologii. 2020; 65(4): 203–11. https://doi.org/10.36233/0507-4088-2020-65-4-203-211 https://elibrary.ru/fxkaqf (in Russian)
- Akimkin V.G., Kuzin S.N., Semenenko T.A., Ploskireva A.A., Dubodelov D.V., Tivanova E.V., et al. Characteristics of the COVID-19 epidemiological situation in the Russian Federation in 2020. Vestnik Rossiiskoi akademii meditsinskikh nauk. 2021; 76(4): 412–22. https://doi.org/10.15690/vramn1505 https://elibrary.ru/zmowbe (in Russian)
- Akimkin V.G., Popova A.Yu., Ploskireva A.A., Ugleva S.V., Semenenko T.A., Pshenichnaya N.Yu., et al. Covid-19: the evolution of the pandemic in Russia. Report I: manifestations of the COVID-19 epidemic process. Zhurnal mikrobiologii, epidemiologii i immunobiologii. 2022; 99(3): 269–86. https://doi.org/10.36233/0372-9311-276 https://elibrary.ru/zxgtfd (in Russian)
- Akimkin V.G., Kuzin S.N., Kolosovskaya E.N., Kudryavtceva E.N., Semenenko T.A., Ploskireva A.A., et al. Assessment of the COVID-19 epidemiological situation in St. Petersburg. Zhurnal mikrobiologii, epidemiologii i immunobiologii. 2021; 98(5): 497–511. https://doi.org/10.36233/0372-9311-154 https://elibrary.ru/dtmnhz (in Russian)
- Belov A.B. The academician V.D. Belyakov – the founder of the domestic theory of epidemiological science of the XXI century. Epidemiologiya i Vaktsinoprofilaktika. 2016; 15(6): 9–15. https://elibrary.ru/xemevf (in Russian)
- Sarkisov A.S. Academician V.D. Belyakov and its contribution to the development of epidemiology. Byulleten’ natsional’nogo nauchno-issledovatel’skogo instituta obshchestvennogo zdorov’ya imeni N.A. Semashko. 2020; (4): 68–72. https://doi.org/10.25742/NRIPH.2020.04.010 https://elibrary.ru/qeazcn (in Russian)
- Zakharov V., Balykina Y. Balance model of COVID-19 epidemic based on percentage growth rate. Informatika i avtomatizatsiya. 2021; 20(5): 1034–64. https://doi.org/10.15622/20.5.2 https://elibrary.ru/zczxuw (in Russian)
- Zakharov V., Balykina Y., Ilin I., Tick A. Forecasting a new type of virus spread: a case study of COVID-19 with stochastic parameters. Mathematics. 2022; 10(20): 3725. https://doi.org/10.3390/math10203725
- Balykina Yu.E., Zakharov V.V. Integral inflow and outflow model and its applications. Prikladnaya matematika. Informatika. Protsessy upravleniya. 2024; 20(2): 121–35. https://doi.org/10.21638/spbu10.2024.201 (in Russian)
- Belyakov V.D., Degtyarev A.A., Ivannikov Yu.G. Quality and Efficiency of Anti-Epidemic Measures [Kachestvo i effektivnost’ protivoepidemicheskikh meropriyatii]. Leningrad: Meditsina; 1981. https://elibrary.ru/zfepwn (in Russian)
Supplementary files