Ретроспективный анализ и прогнозирование распространения вирусов в реальном времени: на примере COVID-19 в Санкт-Петербурге и в Москве в 2020–2021 гг.

Полный текст

Введение

Эпидемия новой коронавирусной инфекции (COVID-19) в Российской Федерации, которая началась в марте 2020 г., вовлекла в эпидемический процесс население всех регионов страны. К концу декабря 2020 г. в стране было зарегистрировано более 3 млн случаев заболевания COVID-19. Такие темпы распространения эпидемии привели к значительному увеличению нагрузки на систему здравоохранения. Вместе с этим во весь рост встала и проблема отсутствия на тот период эффективных методов прогнозирования динамики распространения нового вируса, параметры которого еще не были изучены. По признанию Всемирной организации здравоохранения (ВОЗ), наличие адекватных математических моделей распространения вирусов и разработка методов прогнозирования динамики эпидемий может сыграть ключевую роль при подготовке принятия решений лицами, определяющими ресурсное обеспечение и политику здравоохранения. Такие модели помогают получить представление о будущей динамике распространения инфекционных заболеваний и потенциальной роли разных видов стратегий вмешательства со стороны общественного здравоохранения [1, 2]. Для описания процессов распространения инфекционных заболеваний многие исследователи используют трехкамерную модель SIR. Население страны, в которой распространяется инфекция, разделяется на 3 группы (камеры): восприимчивые к вирусу (Susceptible), инфицированные (Infected) и выздоровевшие или умершие (Removed). Предполагается, что численность населения страны равна сумме численностей этих 3 групп. Впервые модель была в общем виде описана в работе W. Kermack и A. McKendrick в 1927 г. [3], однако наибольший интерес исследователей был в дальнейшем сосредоточен на частном случае этой модели в виде системы из 3 дифференциальных уравнений с постоянными коэффициентами [4]. Некоторые специалисты предпочитают модель SIR из-за небольшого количества требуемых на входе параметров и широких возможностей для применения традиционных классических подходов к моделированию и использованию вычислительных алгоритмов. Однако это преимущество одновременно становится и недостатком, поскольку упрощение модели порождает неточность получаемых на их основе прогнозов по сравнению с фактическими значениями основных переменных эпидемического процесса [5–7]. В ряде статей [8–11] приводятся примеры применения авторегрессионной модели ARIMA при построении прогнозов распространения пандемии в ряде стран мира. Отмечается, что эта модель по сравнению с другими инструментами дает более точные прогнозы, однако, хотя модели временны́х рядов и являются популярным инструментом прогнозирования, их применение для оценки распространения новых инфекций не всегда позволяет построить прогнозы высокой степени точности.

Помимо различных разновидностей моделей семейства ARIMA, для прогнозирования динамики COVID-19 могут также использоваться разные методы машинного обучения, включая деревья решений и ансамблевые модели, такие как случайный лес и градиентный бустинг [12, 13]. Эти техники позволяют учитывать множество факторов, включая уровень заражения, мобильность населения и применяемые меры ограничения социальной дистанции. Искусственные нейронные сети также находят широкое применение, благодаря своей способности обрабатывать временны́е ряды и делать прогнозы на основе последовательных данных [14–16].

Изучению закономерностей эпидемического распространения SARS-CoV-2 на начальном этапе пандемии COVID-19 в Российской Федерации, в Москве и Санкт-Петербурге в 2020 г. посвящены несколько статей [17–20], в которых выделен ряд важных периодов в динамике выявления новых случаев COVID-19: рост заболеваемости, период эпидемического затишья, период осеннего подъема, период устойчиво высокого уровня заболеваемости COVID-19. Следует отметить, что важной мотивацией для проведения настоящего исследования явились в том числе публикации о вкладе академика В.Д. Белякова [21, 22] в развитие представлений о единой («общемедицинской» в его определении) эпидемиологии, включающей неинфекционные заболевания. В более ранних статьях [23–25] авторами настоящей статьи был предложен подход, основная идея которого заключается в прогнозировании сначала будущих прогнозных трендов стохастических параметров эпидемического процесса, а затем в вычислении будущих траекторий основных переменных этого процесса.

Цель настоящей работы заключается в построении прогнозов динамики временны́х рядов случайных значений процентного прироста общего количества заболевших и процентного прироста общего количества выздоровевших и умерших пациентов и описании результатов применения разработанных авторами методов для ретроспективного прогнозирования динамики эпидемических процессов в Санкт-Петербурге и в Москве.

Материалы и методы

Работа выполнена научным коллективом Центра аналитики динамических процессов и систем Санкт-Петербургского государственного университета. При проведении вычислительных экспериментов по прогнозированию динамики эпидемического процесса COVID-19 в Санкт-Петербурге в период с марта 2020 г. по июнь 2020 г. и в Москве с сентября 2020 г. по январь 2021 г. использовали временны́е ряды данных официальной регистрации ежедневного количества новых случаев заболевания и количества случаев завершения болезни (выздоровления или смерти пациентов), представленные на сайте стопкоронавирус.рф и статистические данные Центра CSSE Университета Джонса Хопкинса ¹.

С точки зрения теории математической статистики, данные о новых случаях заболевания образуют временны́е ряды значений x_inf(t) (количество новых случаев в день t), а данные о количестве случаев завершения болезни (выздоровления или смерти пациентов) образуют временны́е ряды x_of(t), где t – это конкретный день эпидемии. Обозначим через X_inf(t) общее количество зарегистрированных случаев заболевания с начала эпидемии до дня t включительно, а через X_of(t) – общее количество пациентов, завершивших болезнь к этому дню. Полученные временны́е ряды X_inf(t) и X_of(t) называются интегральной формой временных рядов x_inf(t) и x_of(t) соответственно. Выраженность тенденции динамики новых случаев заболевания (рост/снижение) принято описывать по методике, предложенной В.Д. Беляковым [26]. Следует отметить, что поскольку члены временно́го ряда x_inf(t) принимают случайные значения, которые могут то возрастать, то убывать, то процентный прирост количества новых случаев, так же как и тенденция роста/снижения, может принимать как отрицательные значения, так и положительные (или равные 0). Процентный прирост числа новых случаев в день t по отношению к числу новых случаев в день t – 1 мы обозначаем r(t) и вычисляем по формуле:

$r\left(t\right)=\frac{x_{\inf }\left(t\right)-x_{\inf }(t-1)}{x_{\inf }(t-1)}\times 100\%$.

Тенденция роста/снижения динамики количества новых случаев заболевания описывается как среднее значение процентного прироста на заданных промежутках времени и используется в качестве важной характеристики при осуществлении мониторинга эпидемического процесса [17]. Однако ее использование в процессе прогнозирования будущей динамики эпидемического процесса в реальном времени представляется проблематичным, в основном ввиду того, что ее значения случайным образом меняют знак с плюса на минус. Можно заметить, что временны́е ряды X_inf(t) и X_of(t), в отличие от временны́х рядов x_inf(t) и x_of(t), являются неотрицательными и возрастают с течением времени. В настоящем исследовании в качестве основных параметров динамики эпидемического процесса рассматривался процентный прирост общего количества заболевших r_inf(t) и процентный прирост r_of(t) общего количества пациентов, для которых болезнь завершилась [23–25]. Значения этих параметров для любого дня t эпидемии можно вычислить по следующим формулам:

$r_{\inf }\left(t\right)=\frac{X_{\inf }\left(t\right)-X_{\inf }(t-1)}{X_{\inf }(t-1)}\times 100\%=\frac{x_{\inf }\left(t\right)}{X_{\inf }(t-1)}\times 100\%$

$r_{of}\left(t\right)=\frac{X_{of}\left(t\right)-X_{of}(t-1)}{X_{of}(t-1)}\times 100\%=\frac{x_{of}\left(t\right)}{X_{of}(t-1)}\times 100\%$

Учитывая, что в числителе и знаменателе представленных формул стоят члены временны́х рядов, указанные процентные приросты тоже образуют временны́е ряды случайных величин. В ходе эпидемии общее количество случаев заболевания и общее количество завершивших болезнь пациентов, как правило, строго возрастают, поэтому значения этих параметров можно считать положительными для любого дня, за исключением дня, в котором число новых случаев равно 0. Кроме того, если процентный прирост r_inf(t) больше процентного прироста r_inf(t – 1), то имеет место неравенство:

$\frac{x_{\inf }\left(t\right)}{X_{\inf }(t-1)}>\frac{x_{\inf }(t-1)}{X_{\inf }(t-2)}$

или, что то же самое:

$\frac{x_{\inf }\left(t\right)}{x_{\inf }(t-1)}>\frac{X_{\inf }(t-1)}{X_{\inf }(t-2)}\ge 1$

Из последнего неравенства можно сделать вывод, что при возрастании процентного прироста общего количества заболевших количество новых случаев заболевания тоже, как правило, возрастает. Однако утверждение, что при убывании процентного прироста общего количества заболевших количество новых случаев убывает, справедливо не всегда.

То же верно и для процентного прироста общего количества выздоровевших и умерших пациентов. Еще одна тенденция, которую можно обнаружить при анализе статистических данных заболеваемости в Санкт-Петербурге и в Москве в мае 2020 г., состоит в том, что снижение процентного прироста общего количества заболевших началось примерно за неделю до наступления пика по числу новых случаев. Эта же ситуация повторилась и в декабре 2020 г. Поэтому мы полагаем, что мониторинг динамики изменения процентного прироста общего количества заболевших имеет существенное значение при прогнозировании динамики как общего количества заболевших, так и новых случаев заболевания.

В рамках настоящего исследования для статистических данных 2020 г. в Санкт-Петербурге и в Москве были построены 20 последовательных 2-недельных ретроспективных прогнозов процентного прироста общего количества заболевших и процентного прироста общего количества пациентов, для которых болезнь завершилась.

Если обратиться к таблице, то можно заметить, что процентный прирост общего количества заболевших в Санкт-Петербурге после 22 апреля 2020 г. имеет явную тенденцию к убыванию. Та же ситуация наблюдалась и в Москве. Аналогичную тенденцию, хотя и менее выраженного характера и с запаздыванием на 2–3 нед, имеет процентный прирост общего количества пациентов, для которых болезнь завершилась.

 

Таблица. Общее количество заболевших COVID-19 в Санкт-Петербурге в апреле–июне 2020 г.

Table. Total number of registered COVID-19 cases in St. Petersburg in April–June 2020

Дата Date	Общее число заболевших, абс. Total number of cases, abs.	rinf(t), %	Дата Date	Общее число заболевших, абс. Total number of cases, abs.	rinf(t), %
12.04.2020	557	14,14	21.05.2020	12 203	3,46
13.04.2020	678	21,72	22.05.2020	12 592	3,19
14.04.2020	799	17,85	23.05.2020	12 955	2,88
15.04.2020	929	16,27	24.05.2020	13 339	2,96
16.04.2020	1083	16,58	25.05.2020	13 713	2,80
17.04.2020	1507	39,15	26.05.2020	14 076	2,65
18.04.2020	1646	9,22	27.05.2020	14 463	2,75
19.04.2020	1760	6,93	28.05.2020	14 846	2,65
20.04.2020	1846	4,89	29.05.2020	15 215	2,49
21.04.2020	1973	6,88	30.05.2020	15 580	2,40
22.04.2020	2267	14,90	31.05.2020	15 949	2,37
23.04.2020	2458	8,43	01.06.2020	16 313	2,28
24.04.2020	2711	10,29	02.06.2020	16 689	2,30
25.04.2020	2926	7,93	03.06.2020	17 069	2,28
26.04.2020	3077	5,16	04.06.2020	17 444	2,20
27.04.2020	3238	5,23	05.06.2020	17 822	2,17
28.04.2020	3436	6,11	06.06.2020	18 169	1,95
29.04.2020	3726	8,44	07.06.2020	18 509	1,87
30.04.2020	4062	9,02	08.06.2020	18 835	1,76
01.05.2020	4411	8,59	09.06.2020	19 153	1,69
02.05.2020	4734	7,32	10.06.2020	19 466	1,63
03.05.2020	5029	6,23	11.06.2020	19 769	1,56
04.05.2020	5346	6,30	12.06.2020	20 043	1,39
05.05.2020	5572	4,23	13.06.2020	20 305	1,31
06.05.2020	5884	5,60	14.06.2020	20 561	1,26
07.05.2020	6190	5,20	15.06.2020	20 813	1,23
08.05.2020	6565	6,06	16.06.2020	21 047	1,12
09.05.2020	6990	6,47	17.06.2020	21 275	1,08
10.05.2020	7404	5,92	18.06.2020	21 506	1,09
11.05.2020	7711	4,15	19.06.2020	21 734	1,06
12.05.2020	8050	4,40	20.06.2020	21 966	1,07
13.05.2020	8485	5,40	21.06.2020	22 195	1,04
14.05.2020	8945	5,42	22.06.2020	22 412	0,98
15.05.2020	9486	6,05	23.06.2020	22 632	0,98
16.05.2020	10 011	5,53	24.06.2020	22 850	0,96
17.05.2020	10 462	4,51	25.06.2020	23 071	0,97
18.05.2020	10 887	4,06	26.06.2020	23 294	0,97
19.05.2020	11 340	4,16	27.06.2020	23 518	0,96
20.05.2020	11 795	4,01	28.06.2020	23 735	0,92

 

Наш метод построения прогноза в конкретный заданный день предполагает на 1-м этапе выбор подходящей функции (линейной, степенной или экспоненциальной) для аппроксимации значений процентных приростов r_inf(t) и r_of(t) за предшествующие 14 сут до дня построения прогноза. После завершения 1-го этапа с помощью выбранной аппроксимирующей функции вычисляются прогнозные значения процентных приростов _inf(t) и _of(t) в течение следующих после дня построения прогноза 14 сут. Полученные значения процентных приростов использовались для вычисления в течение горизонта прогнозирования прогнозных значений _inf(t) и _of(t) по формулам:

${\tilde{X}}_{\inf }\left(t\right)={\tilde{X}}_{\inf }(t-1)\times \left(1+\frac{{\tilde{r}}_{\inf }\left(t\right)}{100}\right)$

${\tilde{X}}_{of}\left(t\right)={\tilde{X}}_{of}(t-1)\times \left(1+\frac{{\tilde{r}}_{of}\left(t\right)}{100}\right)$

Для каждого дня t промежутка прогнозирования можно вычислить отклонение e(t) прогнозного значения от фактического, например:

$e\left(t\right)={\tilde{X}}_{\inf }\left(t\right)-X_{\inf }\left(t\right)$

и абсолютную ошибку прогноза:

$\Delta \left(t\right)=\left(\frac{\left|X_{\inf }\left(t\right)-{\tilde{X}}_{\inf }\left(t\right)\right|}{X_{\inf }\left(t\right)}\right)\times 100\%$

В качестве средней ошибки прогноза для каждого промежутка прогнозирования выбрали часто используемую в статистике ошибку MAPE (mean absolute percentage error). Значения MAPE вычисляли для промежутка прогнозирования длиной 14 сут по формуле:

$MAPE=\frac{1}{14}\sum _{t=1}^{14}\Delta \left(t\right)$

Результаты

Результаты проведенных вычислительных экспериментов представлены в табл. S1‒S8, помещенных в Приложение. В табл. S1–S3 приведены прогнозы динамики процентных приростов общего количества заболевших в Санкт-Петербурге с начала эпидемии, построенные 8 и 22 апреля, 6 и 20 мая, 3 и 17 июня 2020 г.

Средняя ошибка MAPE для прогноза общего количества заболевших, построенного 8 апреля 2020 г., равна 5,15%, 22 апреля – 19,66%. Таким образом, точность прогнозов общего количества заболевших в апреле оказалась не очень высокой. Средняя ошибка MAPE для прогноза, построенного 6 мая 2020 г., равна 4,52% (рис. 1). Следует отметить, что июньские прогнозы, представленные в табл. S3, имеют уже более высокую точность, чем майские. Ошибка MAPE для прогноза, построенного 3 июня 2020 г., равна 3,17%, а для прогноза 17 июня – 0,77%.

 

Рис. 1. Двухнедельные прогнозы общего количества заболевших в Санкт-Петербурге в мае 2020 г.

Fig. 1. Two-week forecasts of the total number of cases in St. Petersburg in May 2020.

 

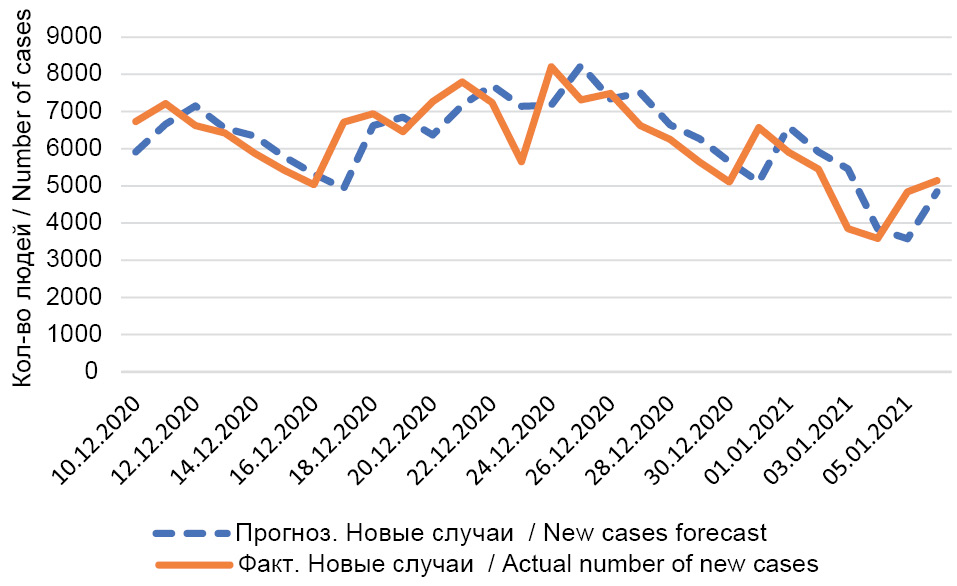
Данные о некоторых прогнозах в осенне-зимний период в Москве приведены в табл. S4 и S5. Ошибка MAPE для прогноза в Москве, построенного 25 ноября 2020 г., равна 0,13%, построенного 9 декабря – 0,13%. Ошибка MAPE для прогноза, построенного 23 декабря 2020 г., равна 0,17%, а построенного 6 января 2021 г. – 0,30% (рис. 2).

 

Рис. 2. Двухнедельные прогнозы общего количества заболевших в Москве в декабре 2020 г.

Fig. 2. Two-week forecasts of the total number of cases in Moscow in December 2020.

 

Как известно, количество активных случаев болезни в любой день можно вычислить, вычитая из общего числа заболевших общее число выздоровевших и умерших пациентов. Прогнозируемое количество активных случаев болезни вычисляли как разность между спрогнозированным общим числом заболевших и спрогнозированным общим числом пациентов, завершивших болезнь. На рис. 3 и в табл. S6 представлены прогнозные и фактические значения количества активных случаев болезни в Санкт-Петербурге в период прохождения пика эпидемии в мае 2020 г. В табл. S7 содержатся данные о прогнозах количества новых случаев заболевания и количества активных случаев в Москве с 24 декабря 2020 г. по 6 января 2021 г. в период прохождения пиков эпидемии (рис. 4, 5). Жирным шрифтом в таблицах выделены максимальные значения фактических и прогнозируемых величин активных случаев болезни в окрестностях пиков эпидемии первой и второй волны.

 

Рис. 3. Прогноз количества активных случаев болезни в Санкт-Петербурге в мае–июне 2020 г.

Fig. 3. Forecast of the number of active cases in St. Petersburg in May–June 2020.

 

Рис. 4. Прогноз количества активных случаев болезни в Москве в декабре 2020 г.

Fig. 4. Forecast of the number of active cases in Moscow in December 2020.

 

Рис. 5. Прогноз новых случаев болезни в Москве в декабре 2020 г.

Fig. 5. Forecast of new cases in Moscow in December 2020.

 

Для того чтобы оценить возможность предсказания резкого роста заболеваемости при распространении штамма Delta в Москве в июне 2021 г., мы обратились к статистическим данным о динамике COVID-19 за этот период. Резкий рост заболеваемости наблюдался с 8 по 15 июня. Мониторинг динамики процентного прироста общего количества заболевших показал, что изменение тенденции устойчивого убывания процентного прироста наблюдалось до 2 июня, затем его значение остановилось на 3 сут на отметке 0,24%, после чего процентный прирост начал возрастать. К 8 июня значение процентного прироста уже достигло уровня 0,32%. Такой быстрый подъем процентного прироста в течение 4 сут, по-нашему мнению, может свидетельствовать о возможном дальнейшем экспоненциальном росте процентного прироста и числа новых случаев заболевания. Ретроспективный прогноз, построенный 8 июня на 6 сут с использованием предлагаемых нами методов, представлен в табл. S8 и на рис. 6. Он имеет ошибку MAPE для общего количества заболевших 0,06%, для новых случаев – 10,41%.

 

Рис. 6. Прогноз новых случаев при распространении штамма дельта в Москве в июне 2021 г.

Fig. 6. Forecast of new cases in during the spread of delta strain in Moscow in June 2021

 

Обсуждение

Как показали вычислительные эксперименты, в апреле 2020 г. динамика процентного прироста общего количества заболевших в Санкт-Петербурге была трудно предсказуема, однако построенные в мае–июне прогнозы оказались уже достаточно точны. Точность полученных ретроспективных прогнозов общего количества заболевших, построенных в мае, значительно возросла по сравнению с апрелем (табл. S2 и рис. 1). Это, по-нашему мнению, объясняется тем, что выбранный метод прогнозирования прошел в апреле стадию обучения на текущих данных и после этого оказался адаптированным к использованию для новых данных, полученных в мае. Из этого можно сделать вывод, что неопределенность в оценке будущей динамики развития эпидемического процесса к началу мая значительно уменьшилась. Эффективность предложенного метода прогнозирования подтвердилась и при построении ретроспективных 2-недельных прогнозов в Москве (табл. S4 и S5, рис. 2). Следует отметить, что в периоды начала распространения более вирулентных штаммов вируса и при введении жестких мер противодействия распространению эпидемии, точность работы предложенного в статье метода может быть ограничена. Такие ситуации требуют дополнительного изучения. В рамках настоящего исследования проводили вычислительные эксперименты по построению 2-недельных ретроспективных прогнозов не только динамики общего количества заболевших, но также были построены прогнозы динамики числа ежедневных новых случаев заболевания, общего числа пациентов, завершивших болезнь, числа активных случаев болезни (текущего числа болеющих людей). Результаты прогнозирования продемонстрировали достаточно высокую точность полученных прогнозов. В качестве примеров в табл. S6 и S7 также приведены данные о прогнозах и фактических значениях количества активных случаев болезни в период прохождения пиков эпидемии в мае 2020 г. в Санкт-Петербурге (рис. 3) и в декабре 2020 г. в Москве (рис. 4). На этих рисунках видно, что спрогнозированные значения количества активных случаев при приближении к пику эпидемии отличаются незначительно от фактических значений. Ошибка MAPE прогнозирования активных случаев болезни в Москве на горизонте прогнозирования 25 декабря 2020 г. – 6 января 2021 г. равна 6,16%. В начальный период подъема заболеваемости фактический максимальный уровень (10 619) болеющих в Санкт-Петербурге был зафиксирован 6 июня, а по прогнозу он составил 12 210 активных случаев болезни и был спрогнозирован на 2 июня. Максимальное число новых случаев в период второго подъема заболеваемости в Москве было спрогнозировано на 25 декабря 2020 г. и составило 8237, а фактическое его значение (8203) было зафиксировано 24 декабря (рис. 5). Ошибка MAPE прогнозирования новых случаев в Москве на горизонте прогнозирования 25 декабря 2020 г. – 6 января 2021 г. равна 15,12%.

Заключение

Анализ динамики ежедневного количества новых случаев заболевания COVID-19 показывает, что это изменение в ходе всей эпидемии имеет стохастический характер, является трудно предсказуемым и, как следствие, создает значительную неопределенность в оценке будущих значений этого показателя и эволюции эпидемического процесса. Рассмотренный в работе метод прогнозирования будущих значений процентных приростов общего количества заболевших и общего количества пациентов, завершивших болезнь, был проверен на статистических данных портала стопкронавирус.рф в период с марта 2020 г. по июнь 2021 г. Построенные в ходе вычислительных экспериментов и описанные в работе ретроспективные 2-недельные прогнозы общего количества заболевших в течение двух пиковых периодов эпидемии, когда нагрузка на систему здравоохранения была максимальной, продемонстрировали достаточно высокую точность. Точность полученных ретроспективных прогнозов общего количества заболевших, построенных в мае, значительно возросла по сравнению с точностью апрельских прогнозов. Это, по-нашему мнению, свидетельствует о том, что выбранный метод прогнозирования динамики процентного прироста общего количества заболевших прошел в апреле стадию обучения на текущих данных и после этого оказался адаптированным к использованию для новых данных, полученных, начиная с мая 2020 г. Применение предлагаемого в работе метода прогнозирования также оказалось достаточно эффективным и при прогнозировании динамики активных случаев болезни и новых случаев в окрестности пиков эпидемии первой и второй волны.

 

¹ COVID-19 Data Visualization Center [Internet]. Johns Hopkins Coronavirus Resource Center. Доступно по: https://coronavirus.jhu.edu/data

Об авторах

Виктор Васильевич Захаров

ФГБОУ ВО «Санкт-Петербургский государственный университет»

Email: v.zaharov@spbu.ru
ORCID iD: 0000-0002-2743-3880

д-р физ.-мат. наук, профессор кафедры математического моделирования энергетических систем

Россия, 199034, г. Санкт-Петербург

Юлия Ефимовна Балыкина

ФГБОУ ВО «Санкт-Петербургский государственный университет»

Автор, ответственный за переписку.
Email: j.balykina@spbu.ru
ORCID iD: 0000-0003-2143-0440

канд. физ.-мат. наук, доцент кафедры математического моделирования энергетических систем

Россия, 199034, г. Санкт-Петербург

Список литературы

Дополнительные файлы