Разработка, изучение и сравнение моделей перекрестного иммунитета к вирусу гриппа с применением статистических методов и машинного обучения

Полный текст

Введение

Общеизвестно, что вирус гриппа А, относящийся к семейству Orthomyxoviridae [1], обладает высокой мутационной изменчивостью, в связи с чем в циркулирующих штаммах (популяции) присутствуют мутантные варианты, избегающие защитного действия антител, которые вырабатываются как в результате перенесенного заболевания, так и вакцинации. Мутантные формы вируса, несущие определенные замены и приводящие к конформационным изменениям поверхностного белка, способны вызывать затруднения во взаимодействии антигенных сайтов с нейтрализующими антителами, что является важным при выборе и оценке штаммов для создания вакцин.

Всемирная организация здравоохранения (ВОЗ) в качестве одного из важнейших критериев оценки успешно проводимой вакцинации и способности предотвращать заболевание у населения рассматривает значения титров антител в реакции торможения гемагглютинации (РТГА)¹. Вместе с тем лабораторно-экспериментальные исследования достаточно затратны по времени и трудоемки. Математическое моделирование перекрестного иммунитета позволяет оперативно выявлять новые антигенные варианты, что имеет первостепенное значение для эпидемиологического надзора и здоровья человека [2, 3].

Перспективным направлением является моделирование распространения вируса гриппа на больших временны́х интервалах, с учетом факторов сезонности и мутаций, для рекомендаций вакцинного штамма на предстоящий сезон. Коллективом НИЦЭМ им. Н.Ф. Гамалеи в 2020 г. была разработана и успешно зарегистрирована компьютерная программа Influenza IDE (эпидемиологическая мультиштаммовая модель (ЭММ)) с моделью перекрестного иммунитета и постоянно обновляющейся базой данных разных видов и подтипов вируса гриппа Influenza DB [4]. ЭММ использует популяционную (агентную) модель для имитации распространения вируса гриппа среди населения, а также вложенные модели (перекрестного иммунитета и иммунного ответа) для формирования иммунного ландшафта (количественного распределения антигенных вариантов с выработанными на них антителами среди населения к рассматриваемому моменту времени в соответствии с индивидуальными историями болезней агентов (индивидуумов)), непосредственно влияющего на скорость и степень распространения отдельных штаммов вируса гриппа среди населения, и на его фоне рекомендует наиболее эффективный вакцинный штамм. Компьютерная программа спроектирована с возможностью интегрирования многочисленных моделей перекрестного иммунитета [5]. В рамках исследований по модификации компьютерной программы коллективом авторов проводятся разработки моделей перекрестного иммунитета на примере вируса гриппа А(H3N2) с использованием математических методов.

Цель исследования – разработка, изучение и сравнение моделей перекрестного иммунитета с применением статистических методов и машинного обучения.

Материалы и методы

Описание данных

Для разработки моделей и расчетов использовался массив данных Influenza DB с информацией из:

‒ опубликованных ежесезонных данных ВОЗ по результатам тестирования сывороток в РТГА (весь массив данных с 2014‒2023 гг.: как референсных, так и тестовых штаммов вируса гриппа А(H3N2));

‒ платформы GISAID (Global Initiative on Sharing All Influenza Data) (последовательности и сопроводительная информация).

После очистки и согласования данных из GISAID с последующим выравниванием на референсную последовательность и объединением в антигенные сайты, согласно предложенному собственному лекалу, формировали матрицу дистанций Хемминга для каждого из 6 антигенных сайтов (с присвоением каждой последовательности уникального идентификатора).

В предыдущих вычислениях [5] с помощью настройки и прогноза на более поздние данные мы показали, что на точность результатов оказывают существенное влияние объем и качество проводимых исследований РТГА. Для разработки моделей перекрестного иммунитета было выбрано подмножество c наибольшим количеством (36 509) наблюдений Cell-Cell (с пассажной историей в культуре клеток). Учитывая принципиальное увеличение наблюдений в 2022 и 2023 гг., мы приняли решение в качестве прогнозных периодов выбрать эти сезоны. А в качестве ретроспективных настраиваемых периодов ‒ промежутки с 2014 по 2021 г., также 2022 и 2023 гг. соответственно (табл. 1).

 

Таблица 1. Характеристика данных

Table 1. Data characteristics

Обучение модели / Model training			Тестирование модели / Model testing
период period	число пар штаммов number of strain pairs	титр titer	период period	число пар штаммов number of strain pairs	титр titer
2014‒2021	10 272	160 [40; 320]	2022	8183	80 [40; 320]
2022	8183	80 [40; 320]	2023	6143	160 [80; 320]
2023 (фев.) / (feb.)	2518	80 [40; 320]	2023 (сен.) / (sep.)	3689	160 [80; 320]
2022 (фев.) / (feb.)	1994	160 [40; 320]	2022 (сен.) / (sep.)	6675	80 [40; 320]

 

В предшествующих расчетах в качестве значений дистанции Хемминга использовали целые числовые значения в соответствии с количеством аминокислотных замен (например, 0, 1, 2, 3 … 8). Для более чувствительного анализа, оценки вклада каждой аминокислоты и сравнения в настоящем исследовании применяли матрицы AАindex. Это база данных числовых показателей, отражающих разные физико-химические и биохимические свойства аминокислот и аминокислотных пар. Тем самым параллельно заменяли значение дистанции Хемминга на присущее числовое значение конкретной физико-химической характеристики.

База данных AAindex состоит из трех разделов и выпускается ежегодно. Матрицы представлены в виде плоских файлов: AAindex1 для индексов аминокислот, AAindex2 для матриц аминокислотных замен и AAindex3 для потенциалов контакта аминокислот. В настоящее время исследователями продолжается сбор и пополнение базы данных с расширением коллекции² [6].

Определение антигенного расстояния и выбор порогов

Общепринятым «золотым стандартом» для оценки присутствия и определения концентрации вируснейтрализующих антител в исследуемых образцах сыворотки является реакция торможения гемагглютинации (РТГА). По сути, в РТГА оценивается уровень перекрестного иммунитета против вируса гриппа [7‒9].

В значительном числе работ по изучению антигенных различий между штаммами (антигенного расстояния) в качестве меры перекрестного иммунитета при инфицировании и/или для изучения эффективности вакцин используют как сами значения титров, так и различные выражения от титров РТГА или логарифмы от этих выражений: Rij = cij / cii [10]; log2(Rij) [11‒13]. При этом определенные значения указанных титров и выражений могут свидетельствовать о наличии или отсутствии защиты против инфицирования конкретным штаммом вируса гриппа. В этом случае переходное значение называют порогом антигенного ускользания. Значения вероятностных порогов антигенного ускользания, выраженных в титрах, основываясь на данных научной литературы, для текущей работы определили как 1 : 40 и 1 : 80 [14, 15].

Кроме того, общеизвестно, что на результаты существенно влияют индивидуальные особенности лабораторных животных. Чтобы уменьшить влияние этих факторов, в качестве порога антигенного ускользания принимается не само значение титра, а соотношение титра рассматриваемой реакции, нормированное на его максимальное разведение для данной сыворотки. В настоящей работе было решено провести расчеты для всего массива тестовых штаммов и взять в качестве порогов антигенного ускользания соотношение максимального значения титра в проведенном эксперименте и значение титра тестового штамма (ref_max/titer) больше 4; и больше или равно 4 [12, 13, 16‒19].

Таким образом, для дальнейших расчетов были применены пороги антигенного ускользания, выраженные в титрах (разведения 1 : 40; 1 : 80), и нормированные (ref_max/titer > 4; ref_max/titer ≥ 4).

Модели перекрестного иммунитета

Для выбранной цели и для решения задач бинарной классификации (антигенного ускользания) рассматривали статистические методы и техники машинного обучения: от простого к сложному, такие как регрессионная логистическая модель, метод случайного леса (random forest) и градиентный бустинг (gradient boosting).

Логистическая регрессия (logistic regression) – тип статистического моделирования, который позволяет количественно связать одну или несколько независимых переменных (предикторов) с бинарным признаком через определение отношения шансов возможных исходов [20].

Метод случайного леса (random forest) – алгоритм машинного обучения, заключающийся в использовании ансамбля деревьев решений. Деревья решений – непараметрический алгоритм, используемый для решения задач классификации и регрессии. Алгоритм работает по принципу древовидной структуры, где каждый внутренний узел представляет собой проверку значения некоторого атрибута, каждая ветвь ‒ результат этой проверки, а каждый листовой узел ‒ метку класса или числовое значение. При классификации методом случайных деревьев объект относится к классу, который выбрало большинство деревьев решений, входящих в ансамбль³.

Градиентный бустинг (gradient boosting) ‒ техника машинного обучения, которая используется для задач классификации и регрессии. Основная идея градиентного бустинга заключается в построении ансамбля слабых моделей, обычно деревьев принятия решений, таким образом, что каждая последующая модель корректирует ошибки, допущенные предыдущими моделями [21]. В рамках настоящей работы для реализации градиентного бустинга была использована библиотека CatBoost⁴.

Для предварительной обработки данных, описательной статистики, обучения и оценки качества моделей использовали библиотеки языка программирования Python:

‒ pandasql 0.7.3 – предварительная обработка данных;

‒ pandas 2.0.3 – описательная статистика, оформление результатов;

‒ sklearn 1.2.2 – логистическая регрессия, метод случайного леса, оценка качества моделей;

‒ matplotlib 3.7.1 ‒ графики.

Анализ стабильности прогностической способности моделей перекрестного иммунитета проводили на основе ретроспективных данных c наибольшим числом наблюдений с последующим прогнозом. В качестве меры адекватности (качества и точности прогноза) моделей и сравнения различных алгоритмов использовали принятые в задачах машинного обучения метрики качества (показатели, которые зависят от результатов классификации и не зависят от внутреннего состояния модели):

‒ Accuracy (точность) ‒ доля воспроизводимости правильных результатов модели;

‒ Sensitivity (чувствительность) (полнота) или доля истинно положительных результатов (true positive rate, TPR), определяется как число истинно положительных классификаций относительно общего числа положительных наблюдений;

‒ Specificity (специфичность) ‒ доля истинно отрицательных результатов (true negative rate, TNR), определяется как число истинно отрицательных классификаций в общем числе отрицательных классификаций;

‒ MCC (коэффициент корреляции Мэтьюса) ‒ сбалансированная мера эффективности, которую можно использовать, даже если один класс содержит гораздо больше выборок, чем другой. Диапазон значений: от −1 до +1;

‒ F1 (F-мера, или F-score) – сбалансированная метрика, объединяющая в себе информацию о точности (preсision) и чувствительности (полноте) с использованием их среднего гармонического значения. Максимизация F1 достигается при одновременном равенстве единице полноты и точности^{5, 6}.

Также использовали ROC-анализ как наиболее объединенный показатель адекватности модели. ROC-кривая показывает зависимость числа верно классифицированных положительных примеров от количества неверно классифицированных отрицательных примеров. Количественную интерпретацию ROC-анализа дает показатель AUC (Area Under Curve, площадь под ROC-кривой). Чем выше показатель AUROC, тем качественнее классификатор. Обычно применяется следующая градация: отлично (0,9‒1,0); очень хорошо (0,8‒0,9); хорошо (0,7‒0,8); средне (0,6‒0,7); неудовлетворительно (0,5‒0,6)⁷, ⁸.

Исследования проводили согласно дизайну, представленному на рис. 1.

 

Рис. 1. Блок-схема исследования. 1.1. Выбор исходных данных; 1.2. Выбор порога антигенного ускользания; 1.3. Разделение данных на обучающий период и прогнозный; 2. Построение моделей; 3. Оценка адекватности и сравнительный анализ. Пояснения в тексте.

Fig. 1. Study flowchart. 1.1. Selection of source data; 1.2. Selecting the threshold for antigen release; 1.3. Dividing the data into a training and a forecast periods; 2. Model development; 3. Adequacy assessment and comparative analysis. Explanations in the text.

 

Результаты

В настоящем исследовании бинарную классификацию, реализованную с помощью разных методов (регрессионная логистическая модель, метод случайного леса (random forest) и градиентный бустинг (gradient boosting)) применяли для предсказания вероятности возникновения определенного исхода (защищен или нет) по значениям титров в разведениях (1 : 40; 1 : 80) или нормированных (ref_max/titer > 4; ref_max/titer ≥ 4).

Пороги, выраженные в титрах (разведения 1 : 40 и 1 : 80)

В расчетах в качестве порогового значения перекрестного иммунитета между двумя произвольными штаммами было решено взять величину титра РТГА в разведении как от 40, так и от 80.

Распределение положительного признака (антигенного ускользания) для порогов 1 : 40 и 1 : 80 как во всех настраиваемых, так и прогнозных периодах варьировалось от 30 до 40% и от 47 до 53% соответственно. Исключение составил 2023 г., в котором для порога 1 : 80 ранжирование этого же признака менялось от 37 до 44%, а для порога 1 : 40 ‒ от 15 до 26%. Подробная информация для всех порогов и периодов представлена в Приложении.

Для каждого временно́го отрезка все три модели настраивали и тестировали согласно дизайну исследования. Результаты расчетов по всем трем моделям в титрах (1 : 40) представлены в табл. 2 и на графиках (рис. 2‒5). Оценку адекватности каждой модели на выбранных прогнозных периодах определяли с помощью общепринятых показателей.

 

Таблица 2. Порог в титрах (1 : 40)

Table 2. Threshold titer (1 : 40)

Параметр Parameter	Accuracy	Sensitivity	Specificity	MCC	F1	AUROC
2014‒2021 => 2022
Лог. регрессия Logistic regression	0,764	0,704	0,858	0,548	0,785	0,859
Случайный лес Random forest	0,803	0,727	0,924	0,635	0,819	0,886
Градиентный бустинг Gradient boosting	0,814	0,750	0,913	0,647	0,831	0,899
2022 (фев. / feb.) => 2022 (сен. / sep.)
Лог. регрессия Logistic regression	0,861	0,804	0,949	0,735	0,875	0,934
Случайный лес Random forest	0,886	0,931	0,815	0,759	0,909	0,958
Градиентный бустинг Gradient boosting	0,880	0,944	0,781	0,747	0,906	0,956
2023 (фев. / feb.) => 2023 (сен. / sep.)
Лог. регрессия Logistic regression	0,637	0,607	0,806	0,297	0,739	0,760
Случайный лес Random forest	0,734	0,719	0,815	0,399	0,821	0,854
Градиентный бустинг Gradient boosting	0,869	0,953	0,402	0,420	0,925	0,851
2022 => 2023
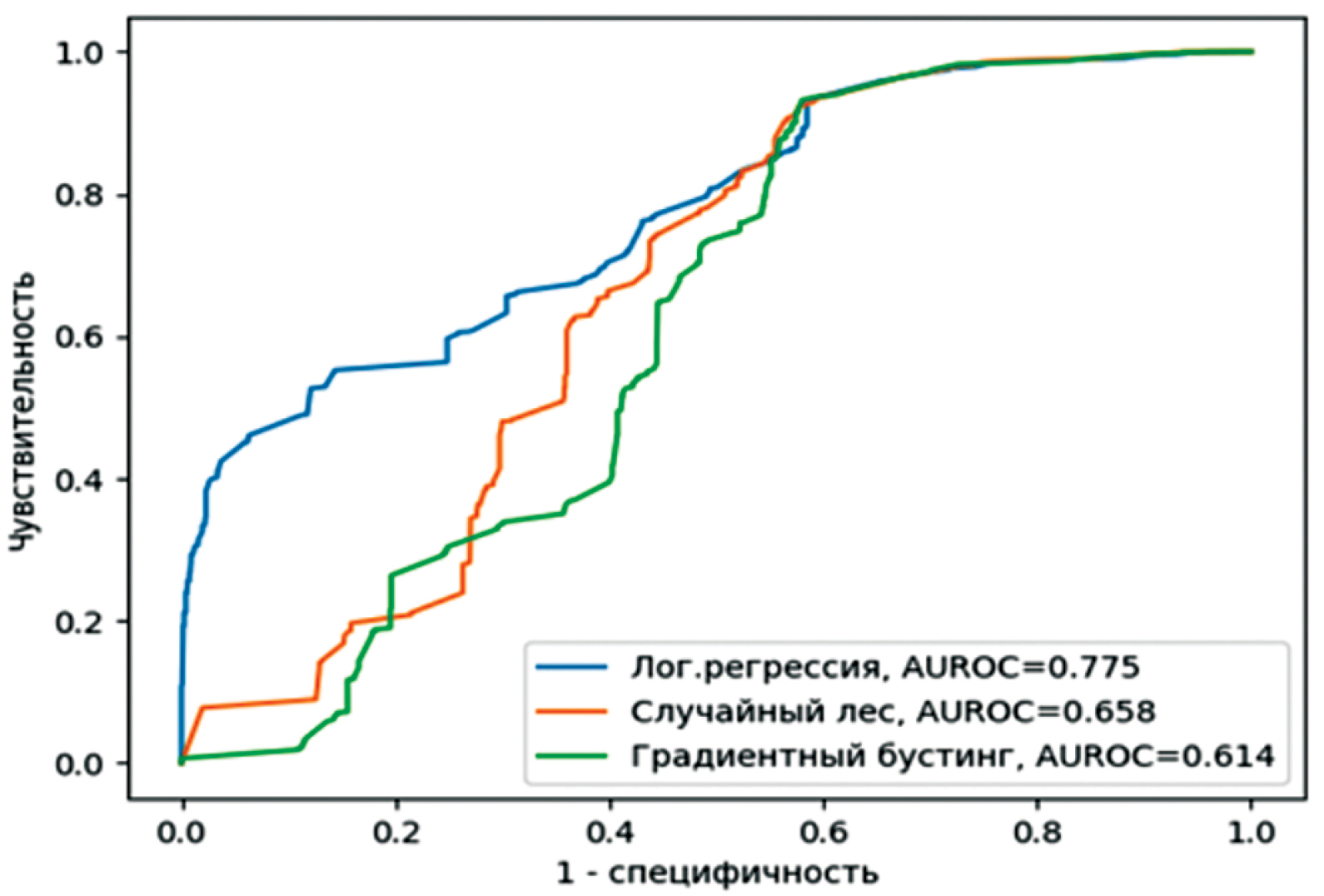
Лог. регрессия Logistic regression	0,837	0,970	0,304	0,393	0,905	0,775
Случайный лес Random forest	0,838	0,968	0,316	0,398	0,905	0,658
Градиентный бустинг Gradient boosting	0,837	0,968	0,311	0,395	0,905	0,614

 

Рис. 2. 2014‒2021 => 2022 (1 : 40). Здесь и на рис. 3‒5: модель логистической регрессии выделена синим цветом; случайного леса ‒ желтым цветом; градиентного бустинга ‒ зеленым цветом, для одного типа порога, выраженного в титрах (разведение 1 : 40). По оси У отложена чувствительность (sensitivity), а по оси Х отложена: 1 минус специфичность (specificity). Пояснения в тексте.

Fig. 2. 2014‒2021 => 2022 (1 : 40). Here and in Fig. 3–5: the logistic regression model is shown in blue; random forest – in yellow; gradient boosting – in green, for one type of threshold expressed in titers (dilution 1 : 40). The sensitivity is plotted on the Y-axis, and the 1 minus specificity represent on the X-axis. Explanations are given in the text.

 

Рис. 3. 2022 (фев.) => 2022 (сен.) (1 : 40).

Fig. 3. 2022 (feb.) => 2022 (sep.) (1 : 40).

 

Рис. 4. 2023 (фев.) => 2023 (сен.) (1 : 40).

Fig. 4. 2023 (feb.) => 2023 (sep.) (1 : 40).

 

Рис. 5. 2022 => 2023 (1 : 40).

Fig. 5. 2022 => 2023 (1 : 40).

 

Как видно из табл. 2, более сложные модели демонстрируют лучший результат практически по всем показателям. Выбиваются из этого ряда с небольшой разницей результаты для прогнозного периода 2023 г., с предварительно настроенным периодом за 2022 г. Что касается сравнения отдельных показателей по всем трем моделям, то следует обратить внимание на величины специфичности и чувствительности. По всем прогнозным и настраиваемым периодам обе метрики сбалансированы. Исключение составляет прогнозный период 2023 г., настроенный на 2022 г., в котором наблюдаются высокие значения для чувствительности и низкие для специфичности.

На рис. 2‒5 представлены результаты ROC-анализа всех трех моделей. Согласно принятой метрике качества классификатора, хорошие показатели под ROC-кривой иллюстрируют все три модели на прогнозный 2023 г. с предварительным обучением на данных за 2022 г. Очень хорошие результаты получились для настроенного периода с 2014 по 2021 г. с прогнозом на 2022 г. Аналогичные результаты показал прогнозный сентябрьский сезон 2023 г., с предварительно настроенным на февральский период этого же года. Достаточно устойчивыми оказались результаты всех трех моделей на прогнозный осенний сезон 2022 г. Обученные на февральском сезоне 2022 г. модели продемонстрировали отличные значения показателей AUROC. Эти результаты совпадают с нашими показателями с применением множественной линейной регрессии [4].

Мы также решили проверить качество наших моделей для порогового значения титра перекрестного иммунитета, равного 80. Подробные расчеты (таблицы, ROC-кривые) представлены в Приложении.

При сравнении результатов, полученных с использованием различных значений порогового ускользания, привлекает внимание тот факт, что вне зависимости от значения порога, при всех настраиваемых периодах, сохраняются тенденции: лучшие результаты получились при прогнозе на 2022 г. и чуть умеренные при прогнозе на 2023 г.

Пороги, выраженные соотношением ref_max/titer >4 и ref_max/titer ≥ 4

Как уже не раз отмечалось исследователями, несмотря на все усилия по стандартизации проведения РТГА [22], изначально заложенная высокая погрешность методики РТГА (17%) [23] остается фактором, существенно влияющим на результаты. Кроме того, на конечный итог существенно влияют индивидуальные особенности лабораторных животных. Чтобы уменьшить влияние этих факторов, в качестве порога антигенного ускользания мы в расчетах применили нормированный ref_max/titre > 4 и ≥ 4.

Наблюдается достаточно ровное распределение положительного признака (антигенного ускользания) для нормированного порога ref_max/titre > 4 как во всех настраиваемых, так и прогнозных периодах ‒ от 44 до 54%. Для нормированного порога ref_max/titre ≥ 4 ранжирование этого же признака меняется от 21 до 28%. Подробная информация представлена в Приложении.

Как видно из табл. 3, сохраняются тенденции с результатами расчетов с применением порога, равного 40. Как и в предыдущем случае, от общего тренда отличаются результаты для прогнозного периода 2023 г., с предварительно настроенным периодом за 2022 г.

 

Таблица 3. Нормированный порог больше 4

Table 3. Threshold normalized more than 4

Параметр Parameter	Accuracy	Sensitivity	Specificity	MCC	F1	AUROC
2014‒2021 => 2022
Лог. регрессия Logistic regression	0,817	0,915	0,714	0,644	0,836	0,840
Случайный лес Random forest	0,816	0,893	0,736	0,638	0,832	0,861
Градиентный бустинг Gradient boosting	0,821	0,900	0,738	0,648	0,837	0,899
2022 (фев. / feb.) => 2022 (сен. / sep.)
Лог. регрессия Logistic regression	0,883	0,929	0,837	0,769	0,888	0,942
Случайный лес Random forest	0,890	0,897	0,883	0,780	0,891	0,951
Градиентный бустинг Gradient boosting	0,890	0,904	0,876	0,781	0,892	0,951
2023 (фев. / feb.) => 2023 (сен. / sep.)
Лог. регрессия Logistic regression	0,750	0,791	0,715	0,505	0,745	0,821
Случайный лес Random forest	0,770	0,840	0,710	0,550	0,771	0,849
Градиентный бустинг Gradient boosting	0,762	0,804	0,726	0,528	0,757	0,848
2022 => 2023
Лог. регрессия Logistic regression	0,624	0,249	0,965	0,310	0,386	0,664
Случайный лес Random forest	0,613	0,257	0,938	0,268	0,388	0,748
Градиентный бустинг Gradient boosting	0,614	0,259	0,937	0,268	0,389	0,725

 

На рис. 6‒9 представлены результаты ROC-анализа всех трех моделей для нормированного порога (> 4).

 

Рис. 6. 2014‒2021 => 2022 (> 4). Здесь и на рис. 7‒9: модели логистической регрессии выделены синим цветом; случайного леса ‒ желтым цветом; градиентного бустинга ‒ зеленым цветом. По оси У отложена чувствительность (sensitivity), а по оси Х отложена: 1 минус специфичность (specificity). Пояснения в тексте.

Fig. 6. 2014‒2021 => 2022 (> 4). Here and in Fig. 7–9: logistic regression models are shown in blue; random forest models are shown in yellow; gradient boosting models are shown in green. Sensitivity is plotted on the Y-axis, and 1 minus specificity represents on the X-axis. Explanations are given in the text.

 

Рис. 7. 2022 (фев.) => 2022 (сен.) (> 4).

Fig. 7. 2022 (feb.) => 2022 (sep.) (> 4).

 

Рис. 8. 2023 (фев) => 2023 (сен.) (> 4).

Fig. 8. 2023 (feb) => 2023 (sep.) (> 4).

 

Рис. 9. 2022 => 2023 (> 4).

Fig. 9. 2022 => 2023 (> 4).

 

На всех прогнозных периодах значения площадей под ROC-кривыми больше 0,8, как и в случае расчетов для порогов, выраженных в титрах (1 : 40 и 1 : 80), за исключением графиков на рис. 9, где величина AUROC больше 0,7 для моделей случайного леса и градиентного бустинга.

Основной причиной меньших показателей AUROC является низкая чувствительность моделей. Следует отметить, что в отличие от типа порога (1 : 40 и 1 : 80) для периода, настроенного на данных 2022 г., и прогноза на 2023 г. логистическая регрессия показывает меньший результат, чем в случае более сложных моделей.

Результаты для нормированного порога, больше и равного 4, в целом аналогичны, для всех периодов, но, как и ожидалось, имеют более высокую чувствительность и слабую специфичность. Особенно заметна разница на прогнозе 2023 г., настроенном на данных 2022 г. Полные расчеты представлены в Приложении.

Применение матриц ААindex

На следующем этапе исследований применяли матрицы AАindex, тем самым заменяя значение дистанции Хемминга на присущее числовое значение конкретной физико-химической и биохимической характеристики. Зарубежные коллеги в своих исследованиях применяли матрицы AАindex в разных комбинациях. Они представлены довольно солидным количеством. И применять все матрицы без подтвержденной теории или логики мы сочли напрасным. Таким образом, было принято решение сначала использовать наиболее часто пересекающиеся матрицы, показавшие лучшие результаты у коллег [24‒27] и далее провести сравнение полученных результатов:

‒ AZAE970101 The single residue substitution matrix from interchanges of spatially neighbouring residues (Azarya-Sprinzak и соавт., 1997).

‒ BENS940104 Genetic code matrix (Benner и соавт., 1994).

‒ MUET010101 Non-symmetric substitution matrix (SLIM) for detection of homologous transmembrane proteins (Mueller и соавт., 2001).

Результаты расчетов по всем трем моделям для порога в титрах (1 : 40) и нормированных больше 4 представлены в табл. 4, 5. Все остальные расчеты представлены в Приложении.

 

Таблица 4. Порог в титрах (1 : 40). Сравнение результатов

Table 4. Threshold titer (1 : 40). Сomparison of results

Параметр Parameter	Дистанция Хемминга Hamming distance	AAindex-AZAE_40	AAindex-BENS_40	AAindex-MUET_40
	AUROC	AUROC	AUROC	AUROC
2014‒2021 => 2022
Лог. регрессия Logistic regression	0,850	0,856	0,857	0,874
Случайный лес Random forest	0,879	0,876	0,878	0,878
Градиентный бустинг Gradient boosting	0,893	0,894	0,908	0,898
2022 (фев. / feb.) => 2022 (сен. / sep.)
Лог. регрессия Logistic regression	0,912	0,887	0,937	0,932
Случайный лес Random forest	0,958	0,956	0,958	0,957
Градиентный бустинг Gradient boosting	0,956	0,957	0,959	0,957
2023 (фев. / feb.) => 2023 (сен. / sep.)
Лог. регрессия Logistic regression	0,772	0,796	0,758	0,790
Случайный лес Random forest	0,854	0,882	0,886	0,884
Градиентный бустинг Gradient boosting	0,851	0,883	0,878	0,875
2022 => 2023
Лог. регрессия Logistic regression	0,790	0,685	0,749	0,737
Случайный лес Random forest	0,659	0,654	0,659	0,649
Градиентный бустинг Gradient boosting	0,624	0,629	0,581	0,590

 

Таблица 5. Нормированный порог больше 4. Сравнение результатов

Table 5. Threshold normalized more than 4. Сomparison of results

Параметр Parameter	Дистанция Хемминга Hamming distance	AAindex-AZAE ref_max/titre >4	AAindex-BENS ref_max/titre >4	AAindex-MUET ref_max/titre >4
	AUROC	AUROC	AUROC	AUROC
2014‒2021 => 2022
Лог. регрессия Logistic regression	0,821	0,833	0,762	0,821
Случайный лес Random forest	0,876	0,881	0,880	0,884
Градиентный бустинг Gradient boosting	0,899	0,884	0,904	0,908
2022 (фев. / feb.) => 2022 (сен. / sep.)
Лог. регрессия Logistic regression	0,936	0,902	0,944	0,943
Случайный лес Random forest	0,950	0,941	0,948	0,947
Градиентный бустинг Gradient boosting	0,951	0,946	0,950	0,943
2023 (фев. /feb.) => 2023 (сен. / sep.)
Лог. регрессия Logistic regression	0,819	0,821	0,820	0,823
Случайный лес Random forest	0,848	0,842	0,846	0,841
Градиентный бустинг Gradient boosting	0,848	0,844	0,849	0,848
2022 => 2023
Лог. регрессия Logistic regression	0,740	0,575	0,644	0,709
Случайный лес Random forest	0,734	0,732	0,739	0,747
Градиентный бустинг Gradient boosting	0,714	0,714	0,676	0,736

 

На основе представленных в табл. 4‒5 сравнительных результатов можно констатировать, что показатели АUROC, рассчитанные как с помощью дистанции Хемминга, так и с использованием выбранных матриц ААindex, существенно не отличаются. Обращает на себя внимание тот факт, что в основном выполняется правило: более сложные модели демонстрируют лучший результат, включая прогноз для периода 2023 г., настроенного на данных 2022 г., с нормированным порогом больше 4. Для вычислений с матрицами ААindex это правило выполняется лучше, лишь с единичными исключениями. Результаты полных исследований представлены в Приложении.

Обсуждение

Основной целью настоящей работы было изучение влияния разных типов применяемых моделей перекрестного иммунитета на результаты исследования. Для более объективной и устойчивой оценки обучали и тестировали разработанные нами модели на разных временны́х периодах. При этом варьировали как тип порога антигенного ускользания, так и его значение.

В основном, как и ожидалось, более сложные модели продемонстрировали лучший результат. Единственный временной период с применением типа порога, выраженного в титрах (1 : 40; 1 : 80), выбивающийся из этой закономерности, ‒ это прогнозный период 2023 г., с предварительно настроенным периодом за 2022 г., где лучший результат показала наиболее простая модель логистической регрессии. В то же время важно отметить, что наши расчеты однозначно продемонстрировали существенное влияние рассматриваемых временны́х периодов, т.е. массивов данных, на результаты прогноза.

Наилучшие результаты прогноза, с применением всех видов моделей и различных типов величин порогов антигенного ускользания были получены на сентябрьский сезон 2022 г., предварительно настроенный на февральском сезоне. Хорошие результаты прогноза на полный 2022 г. продемонстрировали модели, обученные на данных с 2014 по 2021 г. Далее в убывающей градации представлены результаты прогноза на февральский период 2023 г., с настроенным сентябрьским сезоном этого же года. И самые низкие значения показали вычисления на полный 2023 г., с обучением на данных двух сезонов 2022 г.

При сравнении результатов с применением различных типов порогов антигенного ускользания не выявлены существенные отличия. При этом следует отметить, что для значения порогов в титрах (1 : 80) и нормированного больше 4 распределение исследуемого признака антигенного ускользания (положительного исхода) более равномерное, от 37 до 54% соответственно. Несколько другое, более резкое распределение положительного исхода (от 15 до 40%), демонстрируют результаты, полученные для значений порогов в тирах (1 : 40) и нормированного ≥ 4.

Также привлекает внимание тот факт, что при замене величины порога, выраженного как в титрах, так и нормированного, с меньшего значения на большее, в некоторой степени взаимосвязанными выступают два конкретных параметра оценки моделей, чувствительность и специфичность. В расчетах чувствительность увеличивается и уменьшается специфичность.

Впервые очень высокие результаты прогноза на сентябрьский сезон 2022 г., с предварительно настроенной моделью на февральских данных этого же года, были получены в ранней работе [5] с использованием беспрецедентного количества данных за 2022 г. В настоящем исследовании мы повторили расчеты подобным образом, но уже с применением разработанных новых моделей. Дополнительно провели аналогичные расчеты с данными за 2023 г. И в первом и во втором случае получены хорошие результаты. Устойчивость предложенного подхода необходимо проверить на данных следующих сезонов.

Активное использование баз данных ААindex в разработке моделей перекрестного иммунитета было отмечено в ряде научных работ за последние годы [24‒27]. Поскольку матрицы ААindex содержат числовые показатели, отражающие разные физико-химические свойства аминокислот и пар аминокислот, то, предположительно, их использование в расчетах должно привести к улучшению точности модели.

Проведенные нами расчеты с применением трех матриц ААindex, выбранных по принципу наиболее часто пересекающихся матриц в нескольких зарубежных научных работах, не показали существенного улучшения результатов. При этом необходимо отметить, что их применение не ухудшило результаты.

Вышеизложенное может свидетельствовать о том, что для объективной оценки результатов при использовании конкретных матриц ААindex необходимо биологическое обоснование целесообразности их применения в том или ином случае.

В опубликованных к настоящему моменту исследованиях по разработке моделей перекрестного иммунитета авторы обычно используют один набор данных, на которых проводят обучение модели, а на другом множестве данных выполняется ее тестирование. Бывают случаи, когда вся выборка (совокупность данных) случайным образом делится на две части, при этом больший объем предназначен для настройки модели, а меньшее количество для валидации [13, 16, 24, 27‒31]. Результаты текущей работы показывают, что такой алгоритм недостаточен для обоснования предсказательной способности модели. Наши вычисления позволяют утверждать, что результаты достаточно сильно отличаются в зависимости от использованных наборов данных. Чтобы обойти это ограничение и убедительно утверждать о прогностической устойчивости модели, на наш взгляд, необходимо проводить как настройку, так и тестирование на нескольких разных множествах.

Заключение

В рамках текущих исследований разработанные статистическими методами и машинного обучения более сложные модели продемонстрировали лучший результат. При этом выборочное применение типов порогов антигенного ускользания и замена его численных значений не вносят существенного вклада. Их выбор должен обосновываться факторами, независимыми от самой модели.

Для моделей перекрестного иммунитета, основанных на поиске зависимости титров РТГА от изменений в аминокислотных позициях последовательностей вируса гриппа, важно и необходимо проводить обучение и тестирование на различных множествах (наборах данных).

Имеющийся задел знаний и навыки исследователей как в техническом, так и биологическом направлениях позволяют осуществлять дальнейшее развитие моделей перекрестного иммунитета, с применением более сложных техник глубокого обучения.

Финансирование. Авторы заявляют об отсутствии внешнего финансирования при проведении исследования.

Благодарности. Выражаем искреннюю благодарность сотрудникам Центра им. Н.Ф. Гамалеи, главному научному сотруднику Ф.И. Ершову, руководителю отдела экологии вирусов Института вирусологии им. Д.И. Ивановского Е.И. Бурцевой, руководителю лаборатории молекулярной биотехнологии М.М. Шмарову, ведущему научному сотруднику лаборатории физиологии вирусов Института вирусологии им. Д.И. Ивановского И.А. Рудневой за многочисленные консультации в процессе выполнения работы.

Конфликт интересов. Авторы декларируют отсутствие явных и потенциальных конфликтов интересов, связанных с публикацией настоящей статьи.

 

¹ WHO. World Health Organization. Available at: https://www.who.int/initiatives/global-influenza-surveillance-and-response-system (accessed June 24, 2024).

² DBGET/LinkDB в GenomeNet (http://www.genome.jp/dbget-bin/www_bfind?aaindex; ftp://ftp.genome.jp/pub/ db/community/aaindex/).

³ IBM. Available at: https://www.ibm.com/topics/random-forest

⁴ Catboost. Available at: https://catboost.ai/en/docs/ (accessed June 24, 2024).

⁵ Top 10 Machine Learning Evaluation Metrics for Classification ‒ Implemented In R. 2022. Available at: https://www.appsilon.com/post/machine-learning-evaluation-metrics-classification (accessed June 24, 2024).

⁶ F1 Score in Machine Learning: Intro & Calculation. 2022. Available at: https://www.v7labs.com/blog/f1-score-guide (accessed June 24, 2024).

⁷ Метрики качества моделей бинарной классификации. 2023. Available at: https://loginom.ru/blog/classification-quality (accessed June 24, 2024).

⁸ Оценка результатов экспериментов с автоматизированным машинным обучением. Microsoft Learn. 2023. Available at: https://learn.microsoft.com/ru-ru/azure/machine-learning/how-to-understand-automated-ml?view=azureml-api-2

Об авторах

Марина Норайровна Асатрян

ФГБУ «Национальный исследовательский центр эпидемиологии и микробиологии имени почетного академика Н.Ф. Гамалеи»

Автор, ответственный за переписку.
Email: masatryan@gamaleya.org
ORCID iD: 0000-0001-6273-8615

канд. мед. наук, старший научный сотрудник группы эпидемиологической кибернетики отдела эпидемиологии

Россия, 123098, г. Москва

Илья Сергеевич Шмыр

ФГБУ «Национальный исследовательский центр эпидемиологии и микробиологии имени почетного академика Н.Ф. Гамалеи»

Email: shmyris@gamaleya.org
ORCID iD: 0000-0002-8514-5174

научный сотрудник группы эпидемиологической кибернетики отдела эпидемиологии

Россия, 123098, г. Москва

Борис Игоревич Тимофеев

ФГБУ «Национальный исследовательский центр эпидемиологии и микробиологии имени почетного академика Н.Ф. Гамалеи»

Email: timofeevbi@gamaleya.org
ORCID iD: 0000-0001-7425-0457

‒ канд. физ.-мат. наук, старший научный сотрудник лаборатории физиологии вирусов Института вирусологии им. Д.И. Ивановского

Россия, 123098, г. Москва

Дмитрий Николаевич Щербинин

ФГБУ «Национальный исследовательский центр эпидемиологии и микробиологии имени почетного академика Н.Ф. Гамалеи»

Email: shcherbinindn@gamaleya.org
ORCID iD: 0000-0002-8518-1669

канд. биол. наук, старший научный сотрудник отдела генетики и молекулярной биологии бактерий

Россия, 123098, г. Москва

Ваагн Гагикович Агасарян

ФГБУ «Национальный исследовательский центр эпидемиологии и микробиологии имени почетного академика Н.Ф. Гамалеи»

Email: agasaryanvg@gamaleya.org
ORCID iD: 0009-0009-3824-7061

научный сотрудник группы эпидемиологической кибернетики отдела эпидемиологии

Россия, 123098, г. Москва

Татьяна Анатольевна Тимофеева

ФГБУ «Национальный исследовательский центр эпидемиологии и микробиологии имени почетного академика Н.Ф. Гамалеи»

Email: timofeeva.tatyana@gamaleya.org
ORCID iD: 0000-0002-8991-8525

канд. биол. наук, заведующая лабораторией физиологии вирусов Института вирусологии им. Д.И. Ивановского

Россия, 123098, г. Москва

Иван Феликсович Ершов

ФГБУ «Национальный исследовательский центр эпидемиологии и микробиологии имени почетного академика Н.Ф. Гамалеи»

Email: ershovif@gamaleya.org
ORCID iD: 0000-0002-3333-5347

научный сотрудник группы эпидемиологической кибернетики отдела эпидемиологии

Россия, 123098, г. Москва

Элита Русиндапутри Герасимук

ФГБУ «Национальный исследовательский центр эпидемиологии и микробиологии имени почетного академика Н.Ф. Гамалеи»; ФГБОУ ВО «Университет «Дубна»

Email: ealita@mail.ru
ORCID iD: 0000-0002-7364-163X

канд. мед. наук, доцент

Россия, 123098, г. Москва; 141982, г. Дубна

Анна Валерьевна Ноздрачева

ФГБУ «Национальный исследовательский центр эпидемиологии и микробиологии имени почетного академика Н.Ф. Гамалеи»

Email: nozdrachevaav@gamaleya.org
ORCID iD: 0000-0002-8521-1741

канд. мед. наук, заведующая лабораторией неспецифической профилактики инфекционных заболеваний отдела эпидемиологии

Россия, 123098, г. Москва

Татьяна Анатольевна Семененко

ФГБУ «Национальный исследовательский центр эпидемиологии и микробиологии имени почетного академика Н.Ф. Гамалеи»

Email: semenenko@gamaleya.org
ORCID iD: 0000-0002-6686-9011

д-р мед. наук, профессор, академик РАЕН, главный научный сотрудник отдела эпидемиологии

Россия, 123098, г. Москва

Денис Юрьевич Логунов

ФГБУ «Национальный исследовательский центр эпидемиологии и микробиологии имени почетного академика Н.Ф. Гамалеи»

Email: logunov@gamaleya.org
ORCID iD: 0000-0003-4035-6581

д-р биол. наук, академик РАН, заместитель директора по научной работе

Россия, 123098, г. Москва

Александр Леонидович Гинцбург

ФГБУ «Национальный исследовательский центр эпидемиологии и микробиологии имени почетного академика Н.Ф. Гамалеи»

Email: gintsburg@gamaleya.org
ORCID iD: 0000-0003-1769-5059

д-р биол. наук, профессор, академик РАН, директор

Россия, 123098, г. Москва

Список литературы

Дополнительные файлы